Rationale:
In the new Maths GCSE higher tier paper, 30% of marks include a problem-solving element. In my experience, this is something students noticeably struggle with as they are unsure how to tackle this style of question. However, problem-solving as a concept is far reaching. The Education Endowment Foundation’s report, ‘Improving Maths at KS2 and KS3’ recommended that we must ‘teach pupils strategies for solving problems’ (EEF, 2017) as one of its key findings. These skills begin development at primary and continue to be built upon at every stage of a student’s school career. Problem-solving is important beyond just a Maths context, it is a vital life skill that must be developed across the curriculum for us to ensure we are preparing young people to be successful. OFSTED describe the ‘degree of emphasis on problem solving…a key discriminator between good and weaker provision’ (OFSTED 2015).
So what can we do as teachers to help students improve these skills? It is clearly a skill we cannot simply expect students to gain independently and therefore strategies must be explicitly taught to students. I found many potential strategies proposed in various evidence bases. Some general ideas suggested are vital more generally to a successful classroom environment, such as building students confidence, seeing mistakes as a positive thing, and giving time every lesson to develop these skills. More specifically to problem-solving, I have decided to focus on three key strategies; Worked examples, Self-talk and Metacognitive prompts which I will describe next, before considering how these may look in the classroom and future next steps.
Research Summary and Proposed strategies:
1) Worked examples:
This idea is grounded in taking account of cognitive load associated with problem-solving. If problems can be posed in a way that reduces undesirable intrinsic and extraneous load, and instead focuses on germane load, students should be more successful (Renkl and Atkinson, 2003). Teachers can provide students initially with a fully worked example of a problem. They should then provide a minimally different problem, and model some of the solution but let students complete these. Renkl and Atkinson (2003) recommend repeating this process, with modelling being phased out until students are answering questions independently. During this process the question can also become more varied, both in terms of context and structure, as students become more confident with the type of problem being solved, however initially the use of minimally different problems is necessary.
It has been suggested that this strategy could reduce cognitive load to too much of an extent and stop students from being successful when help is removed, as they are too reliant on the worked example and are not actually engaging with the work. This leads to the second proposed strategy, self-talk, as it offers a potential solution to this problem.
2) Self-talk:
Renkl and Atkinson (2003) and the EEF (2017) both recommend the use of this strategy, where students actively engage with a worked example by discussing, explaining the reasoning and method underpinning it with their peers. This can either be in paired discussion or in a whole class setting. It is an effective use for spare cognitive load that is freed up through the use of worked examples. Students must actively engage with the solution given to them and make connections between the question posed and the solution provided, and to understand why that solution is a good/correct one.
The main issue with this strategy is ensuring self-talk is productive and valuable, rather than a distraction or an opportunity for off topic chat. It is also important to find ways of checking the self-talk is accurate. This would potentially be overcome with students sharing their ideas from the discussions with the teacher and rest of the class allowing the teacher to correct as needed.
3) Metacognitive prompts:
Metacognition is thinking about how we think and learn and increasing students’ own awareness of this. This strategy has become popular within educational settings. The EEF’s 2018 guidance on metacognition and self-regulated learning promotes the explicit teaching of metacognitive strategies to students, namely, how to plan, monitor and evaluate their learning. These concepts are mirrored in Polya’s (1945) work on problem-solving skills. He identifies a four-step process to succeed at problem-solving centred around:
– Understanding the problem
– Devising a plan
– Carrying out the plan
– Examining the solution
Polya also suggests making use of prompt questions, that can be adapted to fit different subjects and contexts, to help students master this strategy e.g., ‘what does this connect to?’.
The four steps can be quite a long process, and potentially too long given the time constraints in most schemes of work, but it is important to notice these steps don’t change regardless of the problem being tackled. This would suggest students will become familiar with them and more efficient at moving through the process, ultimately resulting in successful problem solvers. This also would make such a strategy applicable across the curriculum.
Applying to the classroom and what students think:
In Maths


I have trialled all the strategies within Maths. The first example above shows me using worked examples and self-talk to help build students confidence with challenging problem-solving type questions with my middle set Year 11 students. They needed a longer phasing out of worked solutions as they struggled initially with this type of question. By the end of the sequence, I was confident most students could tackle this sort of question, but unsure how they would do with applying the same working to a vastly different problem.



The above example shows a similar approach taken with my top band Year 8 class. You can see the clear difference here is I have included some prompts on the slides that I used to model the solution. This was to help the younger class be able to interpret the worked example successfully during a self-talk phase without errors. With the higher attaining class less phases of modelling were needed and the problems tackled independently could be more varied and students still succeeded.



This example shows a combination of worked examples and metacognitive prompts. The prompt questions seen in the first slide are those I have used with all my classes throughout. The idea being that through using the same prompts, the students become familiar and efficient at using them. The review step is something I would previously have left but gave students the time to reflect on what they had done and secure their understanding.
Overall, the students seemed to like the fact they could succeed with questions at the end of these approaches. It was challenging at times to get students to invest in these processes, particularly those who just wanted to have a go. It is important to be mindful of not squashing this enthusiasm around solving a problem. In terms of when to use each strategy, when a topic was more unfamiliar, students seem to benefit more from a worked example approach, potentially due to the demand on cognitive load with processing a new part of Maths they have not seen before. However, as they became more proficient, they favoured a metacognitive prompts approach as it allowed them to tackle a problem more independently. This suggests that a hybrid of all three approaches is beneficial.
In Science



This example from science highlights the benefit to using minimally different questions with a worked example approach. The first slide shows a modelled 6-mark response written by the teacher live. This was followed by a minimally different question, where the teacher modelled the beginning. Then came a minimally different question with just prompts before finally another minimally different question to do independently. What is also nice about this example is showing where these strategies can fit away from numbers and structured workings. Individual subjects will have their own perception of what problem-solving may look like to them, but the strategies are still applicable.
In Economics
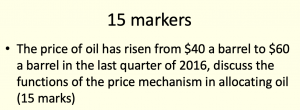
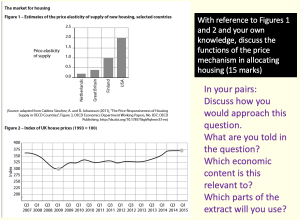


This example again highlights problem-solving in a different setting. Students really struggle with the longer responses in economics and linking the relevant economic content to a question. I first shared a model structure with them before modelling a response. We then used a combination of self-talk and metacognitive prompts to help them come up with their own responses to a minimally different question in terms of content and structure. Lastly students used metacognitive prompts to help them answer a question with the same structure but different context independently.
Next steps:
In order to develop the implementation of explicit teaching of problem-solving skills across the curriculum, its value needs to be seen by both teachers and students. This will ensure they invest the time and effort needed for change to be made. At my school, this has been helped with fortnightly ‘Enrich and Extend’ lessons, where the focus is not on new content, but just on deepening students understanding and exposing them to problems. Hopefully in time, if this can remain a focus, then students will see a noticeable improvement in progress, and will recognise the value of these strategies more. Furthermore, departments must consider embedding these strategies into their teaching practice. In Maths, I have shared these strategies with the teachers in my department. I have also instigated this through building more time into the Key Stage 3 scheme of work to provide more scope for problem-solving in every lesson and re-planned lesson resources to include these strategies explicitly, to ensure they are being utilised. Beyond the Maths department, this is something that must still be considered. As the examples above show, these strategies do help pupils in every setting tackle a challenging non-standard question, with no obvious single answer.
References:
Ofsted (2015) Better Mathematics Conference Keynote Spring 2015. Paper presented at the Better Mathematics Conference, Norwich, Norfolk.
Henderson, P et al. (2017) ‘Improving Mathematics in Key Stages Two and Three’, Education Endowment Foundation.
Quigley, A., Prof Muijs, D., Stringer, E. (2018) ‘Metacognition and Self-Regulated Learning’, Education Endowment Foundation.
Polya G (1945) How to Solve It. Princeton, NJ: Princeton University Press.
Renkl A and Atkinson R (2003) Structuring the transition from example study to problem solving in cognitive skill acquisition: A cognitive load perspective. Educational Psychologist 38(1): 15–22.
Wood, I. (2017) ‘Want to develop your pupils’ problem-solving skills? Here’s the solution’, TES article, 10th October. Available at: https://www.tes.com/news/want-develop-your-pupils-problem-solving-skills-heres-solution-sponsored